Im Technik-Forum gab es vor einiger Zeit eine Diskussion um den optimalen Schaltpunkt zum Erreichen der besten Beschleunigungswerte. Dies sind meine Überlegungen dazu:

a=(3600*P)/(k*m*v)
Dies ist die Gleichung für die erreichbare Beschleunigung eines PKW bei ebener Fahrbahn (P Leistung, k Massenfaktor, m Fahrzeugmasse, v Geschwindigkeit). Vernachlässigt man den Zuwachs der Fahrwiderstände bei steigender Geschwindigkeit v, so ergibt sich, daß die Beschleunigung a linear von der Leistung P abhängt. Die gemittelte Beschleunigung ist damit proportional zum Integral (= Fläche unter der Kurve) der Leistung über der genutzten Drehzahl. Somit läßt sich folgern, daß man den Schaltzeitpunkt so wählen sollte, daß man ständig den Bereich der Höchstleistung ausnutzt. Die folgende Skizze soll dies verdeutlichen:

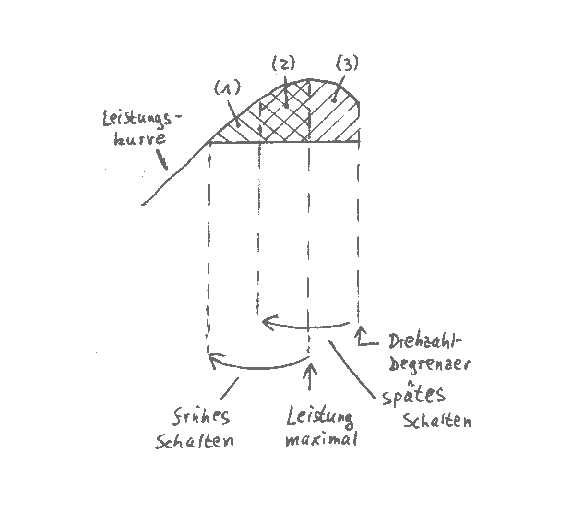
Der ///-schraffierte Bereich (2) und (3) ist die Fläche unter der Leistungskurve beim Hochschalten am Drehzahlbegrenzer. Fläche (1) und (2) (\\\-schraffiert) ergibt sich beim frühen Hochschalten am Punkt der höchsten Leistung. Bereich (2) ist bei beiden Schaltpunkten gleich, also für unsere Betrachtung unerheblich. Nun ist eindeutig zu erkennen, daß Bereich (3) erheblich größer ist als Bereich (1), woraus folgt, daß die mittlere Beschleunigung beim späten Hochschalten größer ist, als beim frühen Hochschalten.
Da die Leistung P=M*2*Pi*n linear von Drehmoment M und Drehzahl n abhängt, das Drehmoment aber selbst nichtlinear von der Drehzahl abhängt, kann man verstehen, warum die Beschleunigung nicht proportional zum Drehmoment ist, sondern wirklich nur proportional zur Leistung. Als Konsequenz dieser Betrachtung folgt, daß man zum Erreichen der bestmöglichen Beschleunigungswerte gerade den VVC Motor bis an den Drehzahlbegrenzer ausdrehen muß.